Twisted Vase in OpenSCAD

Earlier I explained how to use polyhedron to create a regular cylinder in OpenSCAD. Not very exciting but this method is very useful to create much more complex objects. As long as we’re able to find the right function we can create the object with this method.

As an example I’ll explain how to create a twisted or spiraled vase. You’ve probably seen them on Printables or Thingiverse and they exist in many varieties. In this post we first create one starting with a simple triangle and then other regular polygons.

The code in OpenSCAD

For that we use the same method as in the previous post about polyhedron: first we calculate the points of the vase and then we define the faces.

But first consider a regular triangular plane and extrude that in the height (z-direction). Now suppose we twist this triangular plane while extruding and to make it even more complex increase or decrease the size of the plane while extruding. How would that function look like. In this example I’ll use a sinusoid or sine wave function. A sinusoid is the representation of any mathematical sine (or cosine) function that is smooth periodic in nature. Here is the general formula.

f(z) = a + b * sin(c(z)+d);

By substituting values for a, b, c and d we get very different sine functions. In this example I’ll use:

f(z) = 2 + 2 * sin(z)

Before we’re able to calculate our points we need the following variables.

height = 160; //total height of the vase
radius = 30; //radius of the base
step = 1; //steps in z-direction. The lower the more faces
twist = 1.2; //increase to have more twist

The height is in the z-direction, the radius is the radius of the initial circle when all the three vertices of the regular triangle lie on that circle. Step is the step size in the z-direction and twist is the amount of twist that the vase gets. The higher is more twist. Then we need three angles to calculate the exact point of each triangle.

sh3 = [0,120,240]; //triangle

Now we can calculate all the points with the code below

p = [for (z = [0:step:height], angle = sh3) [radius*cos(angle+twist*z)*f(z),radius*sin(angle+twist*z)*f(z),z]];

It’s a nested loop where in the inner loop the angle is varied according to the values of sh3 and in the outer loop the value of z is varied. Hopefully you’ll see similarities the code below that we used in the earlier post to calculate the basic cylinder: [cos(angle) * r, sin(angle) * r, z].

The first two values in the inner square brackets define the position of a point in the xy-plane. Notice that compared with the our earlier formula we multiply x and y values within the brackets with our sine function f(z). We also changed the parameter of the sine and cosine by adding the twist variable and multiply in with z.

Lastly, like we did with the cylinder, we have to create the faces. The code is similar to the code we used with the cylinder but with some essential changes.

module shape(p,m,n) {

    fcs = [for (j = [1:m], i = [0:n-2])[(n*j)+i,(n*j)+1+i,(n*(j-1))+i+1,(n*(j-1))+i]];

    top = [for (i = [n*m:(n*m)+n-1]) i]; //connect points to create the top face

    bottom = [for (i = [0:n-1]) i]; //connect points to create the bottom

    stitches = [for (j = [0:m-1]) [j*n,((j+1)*n)-1,(((j+2)*n)-1),(j+1)*n]]; //connect points between the first and the last face per row

    //now connect all
    //reverse is used to reverse normal of top face
    fcsc = concat([bottom],fcs,stitches,[reverse(top)]); //concatenate the bottom, body and top

    color("teal") polyhedron(points=p, faces=fcsc);
}

The module shape takes as parameters a list of points (p) and the rows and columns of a matrix (m * n). The matrix is calculated as follows.

m = floor(height/step); //numbers of rows of the matrix
n = len(sh3); //number of columns in the matrix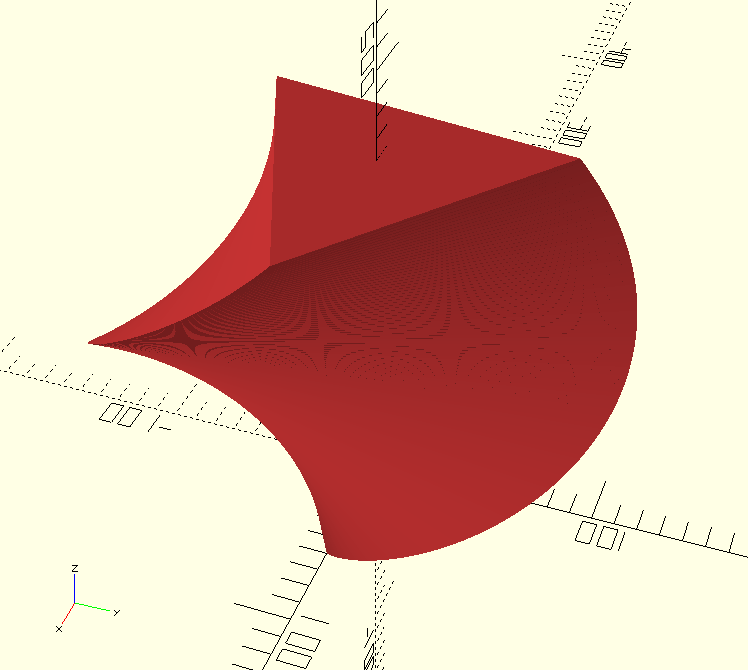

Correcting the normals

Getting back to the shape module you’ll may be noticing that it differs from the cylinder version. One difference is can be found in the fcs list variable. When we watch closely we’ll notice that the for-loop for i has been reversed. This has been done to avoid errors in the stl file. As it turns out the normals of each face from fcs were pointing inwards into the object. OpenSCAD doesn’t complain about it but other programs like Prusaslicer do (see image below).

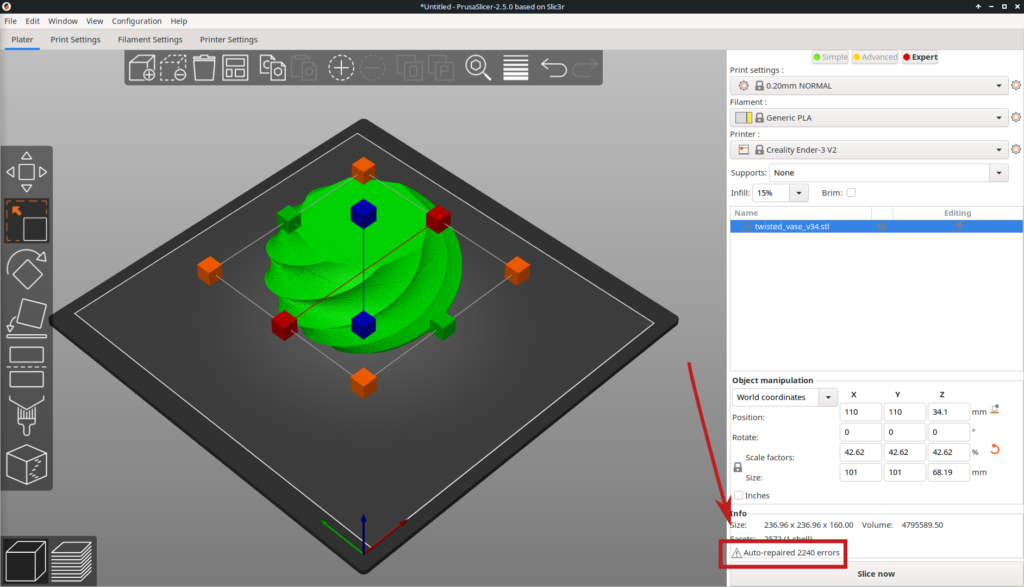
The top also prompted errors and this can be solved by reversing the order of the top list. To do this we need another function called reverse. It reverses the order of the list that is provided as a parameter to it.

function reverse(lt) = [for(i = len(lt) - 1; i > -1; i = i - 1) lt[i]];

Finishing the code

And this leaves only the last part of the code which is simply

shape(p,m,n);

The code that I’ll include with this post is a little more complicated. I added a Customizer to change some of the variables and I added a different sine function (g(z)) that provides a very different vase. I also added the angles for a pentagon, hexagon and octagon (sh5, sh6 and sh8) if you want to change the regular triangle for another regular polygon. If you do make sure to change sh3 on two places in the code: the value for the variable n and in the formula to calculate all points (p).

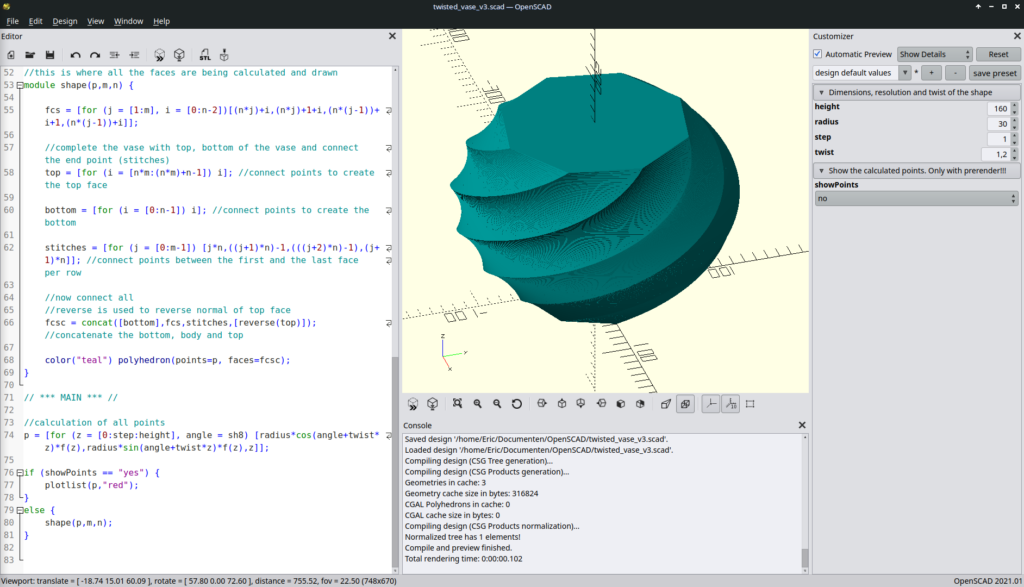
The code can be found in this link: https://eroic42.nohost.me/nextcloud/s/mMbtCciBMA7BEpj.

Thanks for reading!